本篇博客中的公式支持不完整,请您访问这个链接:http://blog.csdn.net/github_35160620/article/details/52684656
在上一篇博客中,我们重点了解了关于自动控制原理的一些基本概念 以及一些相关的术语,以及能够分析控制系统的基本组成以及相应的工作原理。那么本篇博客我们重点学习的是控制原理的数学模型。
我们在上一篇博客中曾经提到过:在经典控制理论当中有三个理论基石:时域分析法,根轨迹法、频域分析法。而这三种方法只是我们分析系统的一种手段,而不管是采用那一钟方法,我们都离不开系统它的数学模型。
数学模型是什么呢? 是我们依据系统的工作原理抽象出来的一些数学表达式或者一些图形。
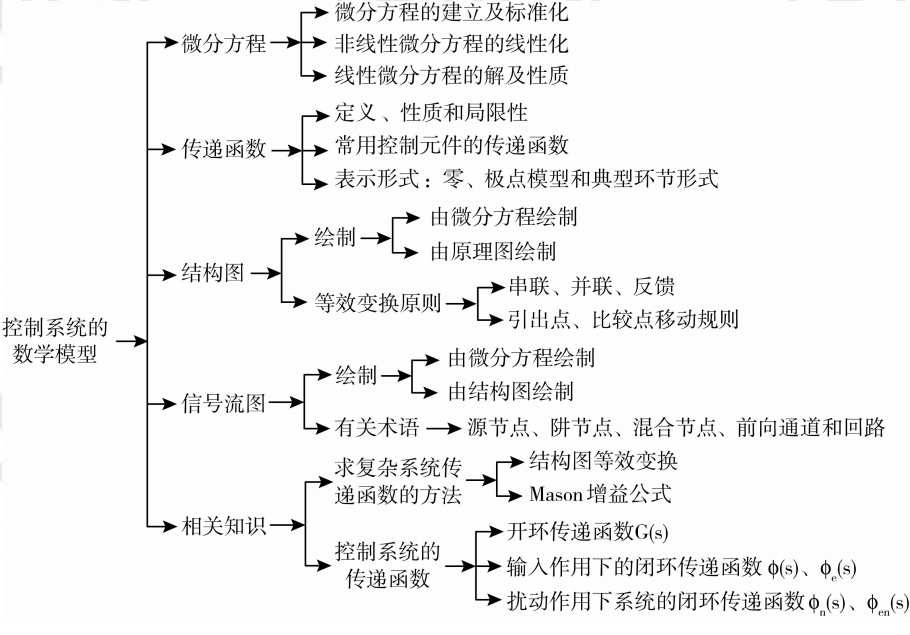
本篇博客中,我们会讲解上面这些数学模型。(微分方程、传递函数、结构图、信号流图)
一 . 微分方程
在时域当中的数学模型,叫做 微分方程。在微分方程这样的数学模型当中,我们要了解一下几个方面:
1 . 微分方程它的建立以及如何化成标准化(什么叫做标准化?所谓标准化是指:我们把微分方程的左右分布安装输出和输入的 各阶导数,以及导数从高到低的次序来排列)。
2 . 此外,微分方程中,除了线性系统之外,还有一些非线性系统的微分方程。(不解释)
3 . 列写这些微分方程的目的是什么呢?我们要通过这些微分方程的解来分析系统的性能。这是我们在时域当中要见到的一种数学模型,这种数学模型(微分方程)它的列写是有一定的技巧的,也就是说我们拿到一些系统以后我们要来分析这些系统它的工作性质,究竟是什么样的系统?是力学系统呢,还是热学系统,还是电学系统。按照这些系统它所依据的物理定律,比如说 :物理学系统它说依据的是牛顿第二定律,而电学系统主要依据的是基尔霍夫电压或者电流定律,列出来原始平衡方程,对这些原始平衡方程进行化解得到标准形式,并且利用微分方程的求解得到微分方程的解,从这些解当中,我们分析控制系统的性能。
二 . 传递函数
在 复频域 当中的数学模型,叫做 传递函数。这种数学模型在经典控制理论当中是站着举足轻重的作用,我们后面的每一篇博客的学习都离不开这种数学模型。
1 . 那么对于这样的数学模型,我们要了解它的定义,以及它的一些性质。尤其是知道了它的性质,在我们分析系统的响应的时候也会起到简化的作用;还有传递函数在描述系统的时候是不是还有一些局限性,这我们也需要了解。
2 . 还需要了解一些常用的控制元件它的数学模型,也就是它的传递函数。
传递函数我们常见的表现形式有几种,这些表现形式有什么样的特点,我们将重点讲两种表现形式。
(1). 一个是以零、极点的模型形式来表现的。我们可以把它写作:一个系统的传递函数 等于 所对应的所有的系统的零点它的乘积 比上 所有的极点它的乘积。这种数学模型在我们后面介绍根轨迹方法当中,经常会见到。
$$G(s) = \frac{K\prod{m}^{i=1}(s - z{i})}{\prod{n}^{j=1}(s - p{j})}$$
(2) . 除了零、极点这种数学模型之外,还有一种数学模型是以典型环节的形式来表述的,也就是说 这个系统的数学模型,我们能够把它写做:传递函数 等于 由一些比例环节或者是一阶的微分环节或者是二阶的微分环节 比上 积分环节或者一阶惯性环节或者二阶的震荡环节等等,这样的形式来表示的,这样的数学模型的形式,我们在频域分析法当中经常会见到。
传递函数这种数学模型在考研当中,求系统的传递函数这样的考题,我们都会见到。所以这种数学模型的形式,我们要非常熟练的掌握。
三 . 动态结构图
除此之外,还有一种数学模型,是以图形的形式来表示的,我们把它叫做:动态结构图。那么动态结构图,我们要掌握它的绘制原则。也就是说:给你一个抽象的物理系统以后,你如何从这样的物理系统当中分析它的工作原理,进而建立它的动态结构图。这种动态结构图的建立是有一定的技巧的,这个我们在后面的博客中会介绍到。那么这种动态结构图的绘制, 绘制出来之后还没有完,我们还需要对动态结构图进行等效,得到系统最终的传递函数,从而分析它的性能。
那么在动态结构图中的等效当中,我们会经常见到这样的几种等效原则: 串联、并联、以及反馈,还有最重要的是:引出点和比较点它们该如何移动。这些我们在后面的博客中也会详细介绍 。
(在各个院校的考研试卷中,动态结构图的题即使不是一专门的题来出现,也会在各种题型中出现,因为从系统的动态结构图建立它的传递函数这一过程,是分析系统的基础,所以这种动态结构图的等效我们也需要牢牢的掌握。)
四 . 信号流图
而动态结构图的等效我们并不提倡大家采用动态结构图化简的方式。因为这种动态结构图化简的方式在遇到了:引出点和比较点相互交叉的时候,经常容易出错,那么我们该怎么办呢? 这在我们下一种数学模型:信号流图的化简 中我们会学习到一钟更简便的方法。
那么信号流图和动态结构图一样都是图形形式的数学模型,那么二者的区别在哪里呢?
信号流图除了可以描述线性系统之外,对于非线性系统,我们一样可以来进行描述。
信号流图的绘制有两种方式:
- 如果一个时域当时的微分方程或者代数方程我们已经知道了,我们就可以从方程当中来绘制它的信号流图。
- 如果动态结构图我们已经知道了,那么我们从动态结构图中,也能绘制信号流图。
其实,信号流图的绘制并不重要,因为我们只要知道了动态结构图,在利用以后会学到的一个公式(Mason增益公式),对于任何系统,它的传递函数都可以很容易的来获得。(Mason增益公式 会在以后的博客中详细的介绍。)
我们刚刚说了:传递函数是控制系统当中非常重要的数学模型,在考试当中会直接或者间接的见到传递函数的求解,这种求解会以什么样的形式出现呢?首先它可能让你去求一个控制系统它的开环或者闭环的传递函数。这在什么情况下呢:给了你动态结构图或者信号流图,那么这就涉及到了动态结构图和信号流图的化简。此外,我们还会见到,比如说:一个系统它是一个多输入的系统,它既有参考输入的作用又有扰动信号的作用,对于这样的系统,分别在不同输入信号的输入下,所对应的传递函数或者是误差传递函数它的求解在考研的各种试题当中也可能见到。
我们重点需要学会的就是这三个问题:
- 传递函数该如何求取
- 动态结构图的化简
- Mason增益公式的使用。
下面我们从重要的知识点开始了解。
五 . 传递函数的定义
刚才我们说过了:在控制系统的数学模型中,传递函数 站着举足轻重的作用,那么什么是传递函数?所谓的传递函数的定义是有这样的前提条件的:
首先:(1)传递函数它针对的是线性的定常系统。那么非线性的系统,或者这个系统是变系数的系统都是不能使用传递函数来表述它的数学模型。
再有:(2)要在零初始条件下。所谓的 零初始条件 是指:在时间 $t=0$ 时刻,输出的各阶导数都应该等于0,并且 $t=0$ 时刻,系统是没有输入的。 这就是零初始条件 的定义。
在满足了这样的两个前提条件的情况下,输出的拉氏变换($C(s)$)和输入的拉氏变换($R(s)$)的比值,我们把它定义为系统的传递函数。
$$G(s) = \frac {C(s)}{R(s)}$$
传递函数和其他的各种数学模型之间还是不割裂的,它们之间是可以相互转换的。比如说,如果现在我们已经知道了时域中的数学模型(微分方程)。这种微分方程和传递函数之间是可以相互转换的 。
下面是一个n阶线性定常系统在时域中的数学模型(n阶的微分方程)。
$$a{0} \frac{d^{n}}{dt^{n}}c(t) + a{1} \frac{d^{n-1}}{dt^{n-1}}c(t) + \cdots + a{n-1} \frac{d}{dt}c(t) + a{n}c(t) = b{0}\frac{d^{m}}{dt^{m}}r(t) + b{1}\frac{d^{m-1}}{dt^{m-1}}r(t) + \cdots + b{m-1}\frac{d}{dt}r(t) + b{m}r(t)$$
这样一个这么长的微分方程,我们只需要把里面所对应的 微分算子 $\frac {d}{dt}$ 全部转换为复频域当中的变量s ( $\frac{d}{dt} \rightarrow s$),那么这样一个微分方程,我们就可以将它转换为系统的一个传递函数了。
当我们将微分方程里面每个微分算子 $\frac {d}{dt}$ 使用 $s$ 替代以后,就变成了下面这样的形式。
$$a{0}s^{n}C(s) + a{1} s^{n-1}C(s) + \cdots + a{n-1} sC(s) + a{n}C(s) = b{0}s^{m}R(s) + b{1}s^{m-1}R(s) + \cdots + b{m-1}sR(s) + b{m}R(s)$$
按照传递函数的定义,零初始条件下,输出(C)和输入(R)的拉氏变换的比值叫做 传递函数。我就得到了相应传递函数的标准形式。
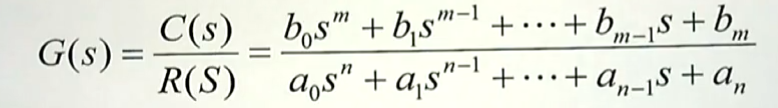
所以,传递函数 和 微分方程 之间是存在一一对应的关系。也就是说,我们要是知道了微分方程,我就可以很容易的获得它的传递函数;反过来,如果传递函数已经知道了,我们只要把其的复变量 $s$ 置换为微分算子 $\frac {d}{dt}$ ,我一样可以得到时域当中的微分方程。
这就是我们提到的传递函数的定义。
六 . 传递函数的性质
传递函数这样的数学模型有着它自身的性质,这些性质对于我们分析系统而言也是非常重要的。这些性质包括以下几种:
1 . 由于现实世界当中能量的传递总是有限的,所以微分方程它的输出端的阶次总是会高于输入端的阶次,那么所对应的传递函数它的分子多项式的阶次就一定会低于(最多能过达到等于)分母多项式的最高阶次,并且我们的传递函数描述的是一个线性定常的系统 ,所以所对应的所有系数都是实数 。
2 . 传递函数描述的是系统输入输出之间的关系式,这种关系式它只取决于系统的绝对参数,而和系统的输入信号是什么是没有关系的。也就是说传递函数是系统的一种固有属性,它和外加的激励是没有关系的,当然和系统的初始条件也没有关系,这在传递函数的定义当中我们就可以了解到,传递函数我们是在零初始条件下来定义的。
3 . 传递函数和微分方程之间是可以相互转换的,因此也是一一对应的,这里也不需要多说。
4 . (做题的时候可能会见到) 传递函数的拉氏反变换是系统的单位脉冲响应。 为什么会是这样呢?传递函数我们是这样定义的:$G(s) = \frac {C(s)}{R(s)}$(输出的拉氏变换与输入的拉氏变换在零初始条件下所对应的比值)
假设外加的激励是一个单位脉冲信号,也就是说:当$r(t)$ 它等于 $r(t) = \delta(t)$ 。那么这个时候,脉冲信号(也叫:冲击信号)就等于 $R(s) = 1$,所以系统的输出的拉氏变换也就等于:$C(s) = R(s)\cdot G(s)$ (输入的拉氏变换和系统的传递函数的乘积),那么这个时候对于复频域当中的方程两侧来去拉氏变换,我们可以得到:在时域当中,单位脉冲信号作用下的时域响应就应该等于:我们对传递函数做一个拉氏反变换。(这个性质在很多的题里面会用到。)
5 . 传递函数只是对系统的数学描述,并不反应系统的物理构成。
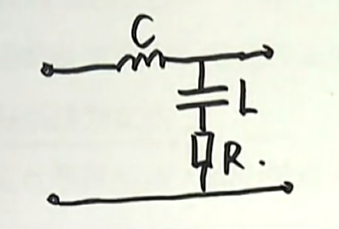
举例:一个是我们在电路当中经常会见到的一种二阶系统(下图),由于电容和电感的存在,两个惯性元件,所以是一个二阶电路,所以在时域当中,描述这个系统的微分方程将会是一个二阶的常系数的微分方程。
再举例:下图是我们经常在力学系统中见到的:一个物体现在在弹簧和阻尼器的共同作用下处于平衡状态,现在加一个外力,原来的平衡被打破,由于这个力学系统当中出现了两个元件(我们认为这个弹簧也好,阻尼器也好,它都是在线性区工作,而且我们认为这个物体可以作为一个集中参数的一个质点来出来),那么这种情况下,描述这个力学系统的数学模型也是一个二阶的常系数的微分方程。
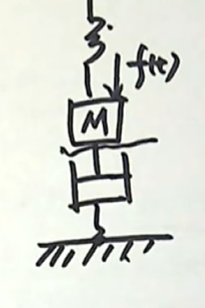
这样两个系统它们的物理形式是截然不同的,所述的领域也不同(一个是 电学中的二阶电路,一个是力学系统中的经典模型),虽然它们的外在表现形式不同,但是由于描述它们二者的数学模型都是一个二阶常系数的微分方程,所以只要这两个系统当中所对应的元件的参数配置恰当,我们完全可以在实验室中用一个二阶电路来分析一个类似的力学系统它的工作性质。
$$a{0}\frac {d^{2}c(t)}{dt^{2}} + a{1}\frac {dc(t)}{dt} + a_{2}c(t) $$
因此我们认为:传递函数只是对系统的一种抽象的数学描述,它并不反应系统的组成,不同形式的系统它可能具有相同的传递函数。
七 . 那么我们如何来建立系统的数学模型呢?
我们可以采用下面这些方法:
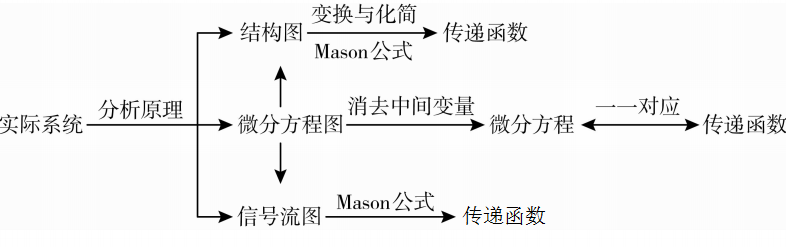
方法1 . 求系统的传递函数,我们可以先分析系统的工作原理,利用它的工作原理列出它的动态结构图,然后利用动态结构图的化简或者是直接在动态结构图当中利用Mason公式,我们可以求得系统的传递函数。
方法2 . 除此之外,如果现在我们得到的数学模型是时域当中的微分方程,只要对这样的微分方程消去中间变量,然后得到一个仅仅与输入和输出有关的这样一个微分方程,我们只要把微分算子使用s来取带,一样可以得到系统的传递函数。
方法3 . 当然,如果系统的数学模型得到的是信号流图,我们可以在信号流图上面直接利用 Mason增益公式 来求解系统的传递函数。
八 . 对于控制类的考生来说最为常见的的控制系统是这样几个:
无源网络(比如:RLC电路)、有源网络(比如:由理想运放搭建而成的模拟电路)、简单的电气控制系统(比如:简单的电力拖动、一些电力控制系统)等。
由于微分方程与传递函数之间存在一一对应的关系,因此我们可以在拿到系统之后,首先先分析系统的工作原理。比如说无源网络,我们可以使用基尔霍夫电压或者电流定律来列写电压和电流之间的微分方程,然后消去中间变量得到系统最终的微分方程;再比如:有源网络。对于有源网络,我们可以使用理想运放的 续断和虚段的性质来列写出有源网络输入和输出之间的关系;再比如:运动控制系统,我们可以利用运动控制系统当中的学到的一些运动的平衡方程来列写它的微分方程。微分方程写出来了,传递函数我就也知道了。
那么如果是有源网络或者无源网络,得到它们的传递函数真的就这么麻烦吗?其实没有这么麻烦。电路不管是有源的还是无源的,我们可以直接利用电路当中复阻抗法来列写系统的传递函数,我们来举个例子:
下面这个图是一个有源网络:输入端是一个电阻元件,输出端是一个电容元件,现在我们来分析它的工作。我们可以这样做:
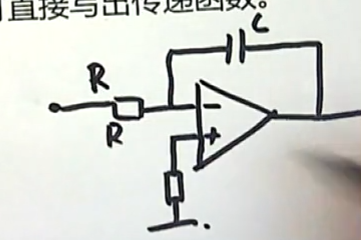
直接在电路中将R和C使用复阻抗来表示:电阻对应的复阻抗仍然是R;电容对应的复阻抗是1/CS。
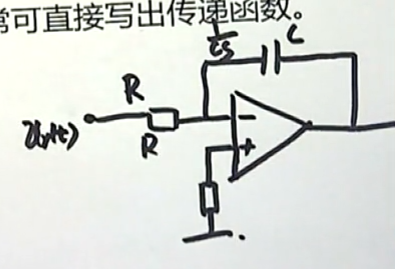
现在想要知道输入输出之间的关系,我们就可以直接得到:(利用理想电路续断和虚段的原理)流出A点的电流等于流入A点的电流。
同时,A点和B点是等电位的,它们的电位都等于0,在这种情况下:
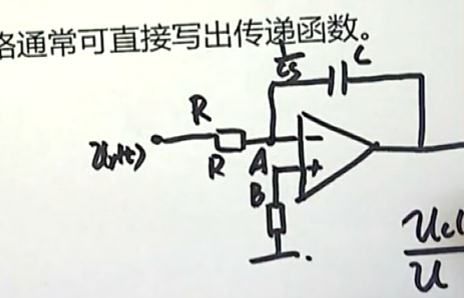
输出和输入的拉氏变换的比值就等于:
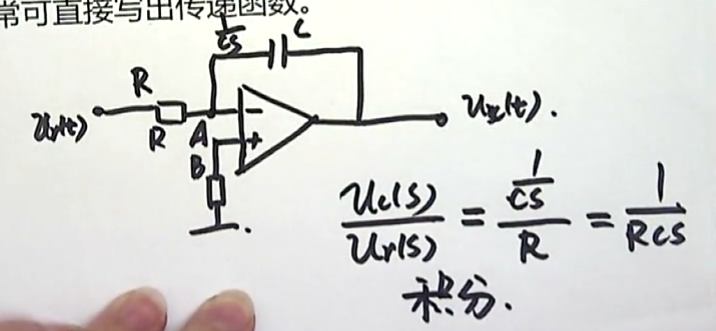
很明显,这样的一个电路完成的功能就是一个:积分器。
所以如果是电网络,我们可以直接使用复阻抗法来求电路的传递函数。
九 . 动态结构图 和 信号流图 绘制
常见的数学模型有两种,分别是:动态结构图 和 信号流图。这两种形式的数学模型是模式系统各个元部件之间的信号传递关系的图型。
这两种图型的绘制是有一定的技巧。
(1)动态结构图的绘制:
我们可以分两步走:
第一步 :化整为零。
在考虑负载效应的情况下,分别列出系统中各元部件的时域方程或复频域方程(代数方程的时域形式与复频域形式相同,微分方程则必须写成复频域形式)
比如:这样的一个二阶的RC电路,如果我们要想绘制它的动态结构图,我们可以将电路划分为两个部分:也就是相当于两个一阶的RC电路。

需要注意:后一阶的RC电路是前一阶RC电路的负载,所以我们需要在考虑负载效应的情况下分别列写系统当中每一个部分所对应的时域方程,或者是复频域方程。(这就是第一步)
第二步:积零为整。
就是说在我们把各个元部件、各个部分所对应的方程列写出来以后,我们按照信号流动的单向性,用信号线把两个部分或诸多个部分之间依次连接起来。
(2)信号流图的绘制
因为很少会让你去绘制信号流图,所以这一部分我们不讲。
十 . 动态结构图的变换与化简
对于动态结构图,它的基本连接方式有三种:串联、并联 和 反馈 。它们所对应的化简是比较简单的。
动态结构图的变换和化简只是一种手段而已:通过动态结构图变换,使系统当中只出现三种基本形式(下面会讲)以后,我们就可以直接来求解系统的传递函数了。
当然,在结构图的变换和化简当中,我们只能减少(或者增加)一些中间变量,但各变量之间的数学关系不能改变。
最常见的变化方式:
1 . 比较点前移

比如说:
在比较点前移之前,系统的输出等于:(上上图)
$$X{3}(s) = X{1}(s)\cdot G(s) \pm X_{2}(s)$$
而在做了比较点前移的变换之后,系统的输出等于:
$$X{3}(s) = [X{1}(s)\pm X{2}(s)\cdot \frac {1}{G(s)}] \cdot G(s)$$ $$ = X{1}(s)\cdot G(s) \pm X_{2}(s)$$
也就是说,在我们做出等效变换之后,系统的输出是没有发生过改变的。
2 . 比较点后移
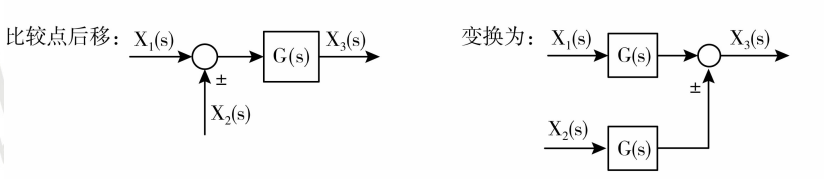
比较点前移也好,后移也好,这些等效变换,我们要掌握的一个原则是:在变换前后系统的输出没有发生改变。
比较点的前移和后移,以至于引出点的前移和后移,这个都没有问题。
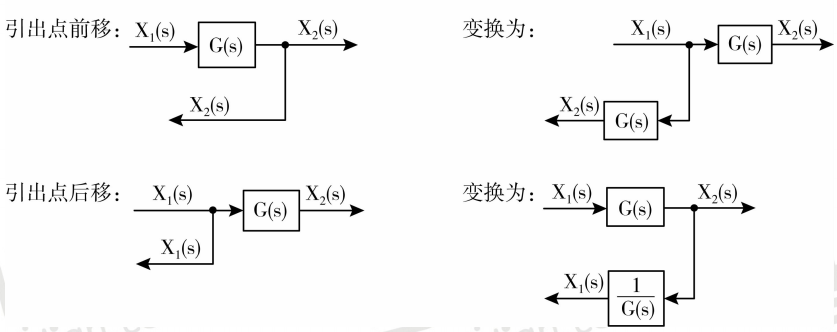
但是在做动态结构图化简的题型中要特意注意一个问题:如果遇到了比较点和引出点相互交叉的情况,那么在这种情况下,不适于采用化简的方式对动态结构图做简单。那么我们可以怎么做呢?
我建议大家熟练的掌握 Mason公式 ,Mason公式可以直接从动态结构图或者是信号流图当中求出来系统的传递函数。这样情况我们只需要找清楚(从输入节点到输出节点的)前向通道,找清楚 独立回路,这个时候牢记Mason公式,将会使我们的解题得到极大的简化。
(现在先不讲 Mason公式)

十一 . 考研要点
1 . 如何建立控制系统的微分方程(有源网络和无源网络如何列写它的微分方程)
2 . 传递函数的概念、性质以及表示形式(表示形式有两种:零、极点的表示形式(跟轨迹增益); 典型环节相互串联的形式(系统增益))
3 . 动态结构图的等效变换
4 . 求复杂系统的传递函数
在下一讲中,我们针对本篇博客的重要知识讲讲一些例题。通过这些典型的例题,对知识点进行巩固。