本篇博客中的公式支持不完整，请您访问这个链接：http://blog.csdn.net/github_35160620/article/details/52938197
这篇博客，在上一篇的基础上，针对 自动控制的数学模型 的重要考点，举一些典型的例题，加以解析，巩固大家对 自动控制的数学模型的掌握。
PID调节器 — 自动控制原理中最简单、最经典、最有用的调节器
我们先来看第一道题：
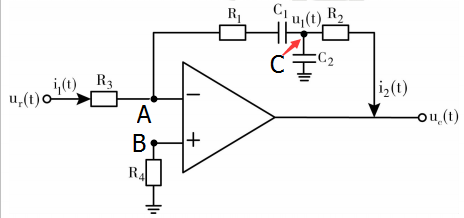
一有源网络如下图所示，要求：
- 写出系统的微分方程；
- 求系统的传递函数；
- 说明此电网络在校正中的作用。
解：
这一道题，给了一个有源网络，要求建立它的两种形式的数学模型（一种是在时域当时所对应的微分方程；还有一种是复频域当中所对应的传递函数）。并且让我们分析：如果这个电网络放在了系统当中，将会给系统的性能产生何种的校正作用。
这种类型的题，我们会经常见到。要么是以有源网络的形式，要么是以无源网络的形式出现。 要解决这样的一类问题，一般有两种方法。
第一种方法：先写出在时域中所对应的微分方程组。比如是针对这样的有源网络而言，我们要充分利用到这个理想运算放大器它的续断和虚段的原理，根据：流入A节点的电流和流出这个节点的电流相同，同时在运算放大器的同向和反向输入端又没有电流流入。这样的话，我们可以在时域当中列出它的方程，然后消去中间变量。最终得到一个只和输入和输出有关的微分方程。
还有一种方法，是我们在上一篇博客当中提醒大家，在考试中经常会使用到的方法。这种方式是这样的：不管是有源还是无源网络，我们都可以利用复阻抗的方法，将电网络当中所对应的电阻、电感、电容用复阻抗来表示，然后用运算法直接列出复频域当中所对应的方程组，然后在直接的消元或者结合框框图，求出系统的传递函数。
一般情况下，遇到的电网络，不管是有源还是无源，我们都提议使用第二种方法会比较简单。
我们现在来看看这道题。对于这样的有源网络而言。由于表述这个系统的数学模型：微分方程和传递函数之间是可以相互转换的，所以我们不管是求出来哪一种形式的数学模型，传递函数也好、微分方程也好，只要求出来一种，另外一种也就没有问题了。对于这样道题，我们来看看。
首先我们把这个有源网络当中所有的R、C 全部用 复阻抗 的形式来表示。所对应的电阻是不变的，而电容将它转换为 $\frac {1}{CS}$ 。这样，不管是输出信号、输入信号就都可以使用复频域的形式来表示了。
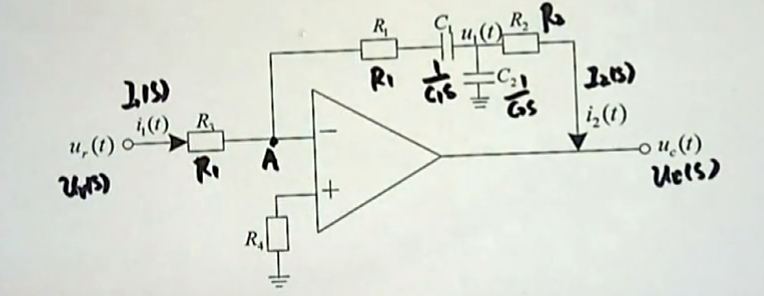
当把电路转换为这样的形式之后，我们就可以接着往下做了。对于 A 点而言，由于流入它的电流等于流出它的电流。所以我们有：
$$\frac{u{r}(s) - u{A}(s)}{R{3}} = \frac{u{A}(s) - u_1(s)}{R{1} + \frac{1}{C{1}S}}$$
（这样就得到的复频域里面的第一个方程了。）
我们在往下看 ，对于C点而言，这是一个电网络，所以对于C 点，我们一样可以利用基尔霍夫电流定律：流入 C 点的电流应该等于流出 C 点的电流之和。
$$\frac{u{A}(s) - u_1(s)}{R{1} + \frac{1}{C{1}S}} = \frac{u{1}(s) - 0}{\frac{1}{C{2}S}} + \frac{u{1}(s) - u{C}(s)}{R{2}}$$
这样对于 A 和 C 这两点而言，我们都列写出来的它们所对应的电流平衡方程，而理想的有源运放同时又满足：A 点 和 B 点 是等电位的，等于0。
$$u{A} = u{B} = 0$$
这样的话，由这样的三个方程，我们消去中间变量，$u_{1}(s)$、$u_{A}(s)$，这样可以得到下面的关系式：
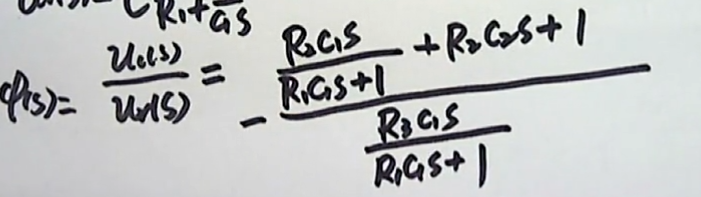这里有一个负号，这里我们要做一个特别说明 ：由于现在这个题中的有源运放的输入信号是加在反向输入端（$-$），所以会有一个负号存在，但是这样的一个元器件，或者说这样的一个有源网络加在电路当中以后，我们知道信号一旦进过它（有源运放的反向输入端）以后，会产生一个反向作用就可以了，我们并不需要再传递函数当中额外的留意负号的存在，所以这个传递函数，我们可以进一步将它化简为：
系统的传递函数，最终化简得到：
一旦这个有源网络给定了，所以 R1、R2、R3的参数也就确定下来了。所以这个组合，只要有源网络不变，它们的 组合的值就不会发生改变，在典型环节当中，我们认为它是一个比例环节 （P）
而公式中间的部分，我们观察它，它是一个：一个常数 乘以 一个所对应的微分环节，我们在典型环节中把它叫做：微分环节（D = ($K_{I}S$)）
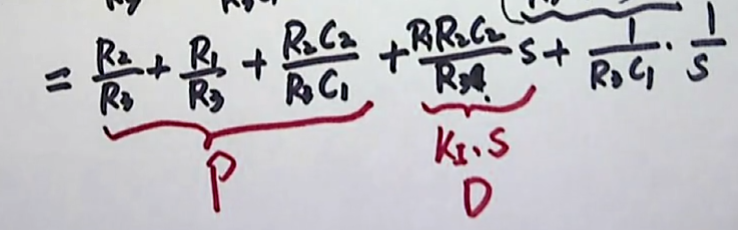
在来看最后一部分，我们可以将它写做：$K_{I}\frac{1}{s}$ 。相当于一个积分常数 与 积分环节相乘。典型环节当中，我们把它叫做积分环节（I）。
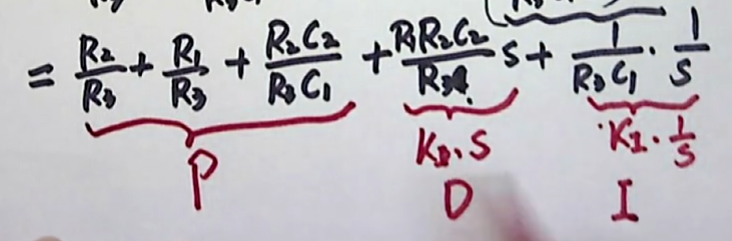
所以，这样的一个有源网络，它们组合起来以后，形成了一个经典控制理论当中最重要的调节器：我们把它叫做：PID调节器。
这个PID可以这样来理解：在经典控制理论当中，我们所有的问题基本上，都是围绕着这样的一种调节器展开的，而这种调节器在整个控制领域的应是非常非常的广泛。
好，现在我们已经建立了这个图中有源网络的传递函数，并且分析了这样一个有源网络在系统当中实际上就是一个PID调节器。那么这个PID调节器的每一个部分对系统性能的影响表现在哪里呢？
首先，我们来看P 比例部分。比例部分的存在可以改变一个系统的系统增益，而一个系统的系统增益发生了改变，那么所对应的稳态性能（比如说：是否稳定），或者稳态误差的大小，都有可能会改变。
而微分部分的存在，它可以加快系统的响应速度。
而积分 部分的存在，它可以降低系统的误差。
所以，每一个部分在系统中的影响，你需要格外的清楚，当然PID调节器，我们在日后的博客中，还会再次介绍。
当我们建立起来了系统的传递函数以后，再想求它时域当中的数学模型 — 微分方程，就没有什么困难了。我们可以将传递函数当中所有的 复变量s用微分算子 来代替。也就是说，把所有的s置换成$\frac {d}{dt} \leftarrow s$
我们可以得到传递函数 将上面的比例部分使用$K{P}$ 来表示、微分部分使用$K{D}s$来表示、积分部分使用$K_{I} \frac {1}{s}$来表示。
$$\varphi (s) = \frac {u{c}(s)}{u{r}(s)} = K{P} + K{D}s + K_{I} \frac {1}{s}$$
现在，我们就可以还原回时域当中。这样，我们就可以得到时域当中所对应的微分方程：
$$u{c}(t) = K{P}u{r}(t) + K{D} \frac {du{r}(t)}{d{t}} + K{I}\int u{r}(t)d_{t}$$
（当然，在微分方程当中，积分符号的存在，在微分方程中是不常见的。所以，我们可以对微分方程的两侧再求一次导。） 可以得到：
$$\frac {du{c}(t)}{dt} = K{P} \frac {du{r}(t)}{dt} + K{D} \frac {d^{2}u{r}(t)}{dt^{2}} + K{I} u_{r}(t)$$
那这样是一个微分方程是不是我们时域当中微分方程的标准形式呢？不是。 微分方程应该在右侧的公式里面，通过求导从高到底的形式来表示。
$$\frac {du{c}(t)}{dt} = K{D} \frac {d^{2}u{r}(t)}{dt^{2}} + K{P} \frac {du{r}(t)}{dt} + K{I} u_{r}(t)$$
所以现在，我们得到了一个二阶的常系数的线性的微分方程。这是这个有源网络在时域当中所对应的数学模型（微分方程）。
第2道
我们上一篇博客里面有说过：如何来建立系统的动态结构图。我们说过：可以分两步走：第一步：化整为零；第二步：积零为整。
所谓化整为零：把一个复杂的系统划分为若干个子系统，列出来每一个子系统所对应的微分方程或者复频域当中的代数方程。要注意的是：前后两个子系统之间是不是存在信号的彼此联系，也就是说：后一个子系统是不是前一个子系统所对应的负载。在完成了化整为零这一步之后，就开始做积零为整这一步，我们需要按照信号流动的单向性把我们所对应的环节相互连接起来，构成我们整个系统的动态结构图。
我们现在解的这道典型例题，系统不再是以原理图的形式给你了。而是以微分方程或者是代数方程的形式给你的，那么系统的微分方程一旦了解以后，我们应如何建立系统的动态结构图？并且进一步求取系统的传递函数呢？并且在传递函数中，我们要注意，这个系统的传递函数不止一个： $\frac {C(s)}{R(s)}$ 、$\frac {C(s)}{N{1}(s)}$、$\frac {C(s)}{N{2}(s)}$
这些传递函数，我们来观察一下，从它的表型形式，我们发现。这道题最终得到的动态结构图，它的输入信号肯定是不止一个的，它既有给定参考输入$R(s)$，同时也会存在扰动输入$N{1}(s)$、$N{2}(s)$ ，那么对于此类的题型，我们要如何解决呢？ 其实这种问题也非常简单。我们来观察一下这一组微分方程，在我们动态结构图当中，常见到的组成部分有这样几个：
比较环节
所谓的比较环节，是指两个或者两个以上的信号在这一点相遇以后，（什么点？比较点，我们使用小圈来表示。）所对应的比较点的输出（输出将会是输入信号的叠加）。
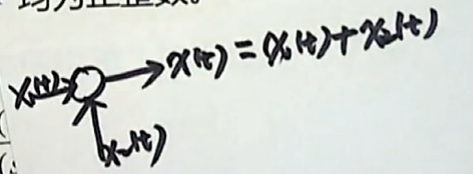
除了比较点之外，再我们的动态结构图当中，还有一个重要的组成部分：方框：
而方框的存在相当于一个乘法器。它表示：任意的信号在经过方框以后，所对应的输出都应该用这个信号乘以方框所对应的传递函数。
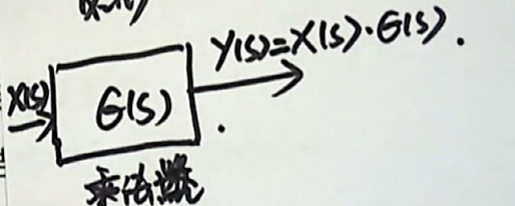
动态结构图除了这两个组成部分之外，还有一个组成部分，我们把它叫做：引出点。
引出点是指：从同一个信号线上面的不同位置引出来几路信号，而引出来的这几路信号它的大小、性质是完全一样的。
我们的动态结构图也就这三个基本组成部分。那么这三个组成部分对应我们微分方程中运算是什么呢？
比较点：对应 加减运算。
方框： 对应 乘法运算。
引出点：相同的信号，从哪个位置出来，我们就清楚了。
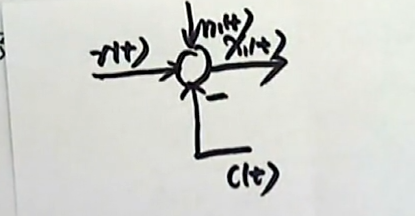
现在我们回到这道题当中来，我们来看看第一个微分方程（$x{1}(t) = r(t) - c(t) + n{1}(t)$）。这个微分方程实质上是一个代数方程。在这个方程中只涉及到了加和减的计算，这个计算在我们动态结构图当中，实际上就相当于只遇到了比较点。
这个比较点的输出信号我们假设是 $x{1}(t)$ ，这个比较点的信号是有三路信号叠加而成的，一路我们假设是参考输入信号$r(t)$，还有一路是来至于系统的输出$c(t)$ 。注意 $r(t)$ 和 $c(t)$ 之间是减的关系，所以$c(t)$ 在这里有一个负号；此外，还有一路信号是来至 $n{1}(t)$。
现在，我们就利用了一个比较点，将第一个代数方程所描述的关系已经表达出来了。
怎么由$x{1}(t)$得到$x{2}(t)$？
它是经过了一个比例环节（$x{2}(t) = K{1}x{1}(t)$），也就是说 $x{1}(t)$ 这个信号经过了K1 倍的放大以后，得到了 $x_{2}(t)$。
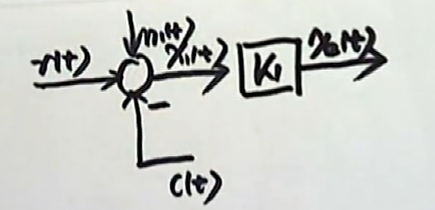
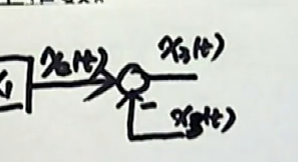
再来看第三个方程（$X{3}(t) = x{2}(t) - x_{5}(t)$），第三个方程仍然涉及到的是一个叠加运算。仍然是遇到了一个比较环节，这个比较环节是哪两个信号进行比较呢？
$x{2}(t)$ 和负的 $x{5}(t)$ 。这两路信号在这里做了一个比较。比较以后的输出是 $x_{3}(t)$。
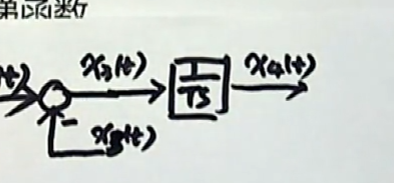
继续看第4个方程（$T \frac {dx{4}(t)}{dt} = x{3}(t)$）。 如何从$x{3}$ 变成 $x{4}$ 呢？
我们可以考虑对这样的式子做一个变形。 我们将它转换到复频域当中，这样，我们有：
一阶微分对应的是一个 s。也就是说，如果我们想通过 $x{3}$得到$x{4}$，实际上，我们需要经过一个环节的传递，这个环节是一个积分环节。我们现在把这样的积分环节带到动态结构图当前去。
$x{3}(t)$ 经过了一个积分环节（$\frac{1}{TS}$）之后，得到了一个输出信号： $x{4}(t)$。
在来观察一下第5个方程（$x{5}(t) = x{4}(t) - K{2}n{2}(t)$）：
在这个方程当中，所对应的输出信号是$x{5}(t)$，这个方程又是两路信号的叠加。
哪两路呢？一路是来至于 $x{4}(t)$，还有一路是来至于$n{2}(t)$，并且这个$n{2}(t)$ 是经历了一个比例环节 $K{2}$，这样的两个环节相互比较得到了输出信号 $x{5}(t)$
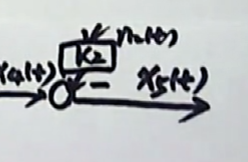
最后一个方程（$K{0}x{5}(t) = \frac {d^{2}c(t)}{dt^{2}} + \frac {dc(t)}{dt}$）。最后这个方程里面仍然有微分符的存在。我们在动态结构图当中，每一个方框里出现的只能使传递函数，所以，我们要这个微分方程所对应的传递函数找到。它的传递函数是什么呢？
现在这个环节，它的输出是$c(s)$ ，输入是$x_{5}(s)$ 。从这个方程中我们可以得到：
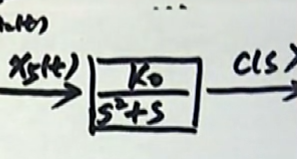
传递函数就是这样的： $G(s) = \frac {K_{0}}{s^{2} + s}$。
现在我们就发现了。从 $x_{5}(t)$ 经过一个二阶环节以后得到的整个系统的输出 $c(s)$。
我们现在来观察一下整个系统的动态结构图。在前面也有一个 $c(t)$。最后一步就是：相同的信号进行合并。同理$x_{5}(t)$ 的两个信号线也要进行合并。
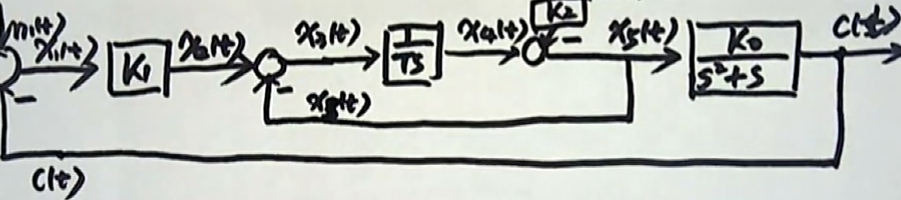
这样整个系统的动态结构图，我们就画出来了。
再画结构图的时候，大家要注意一点：如果在遇到微分符号的 存在，就是给你的是微分方程，你需要先把它单个的微分方程做拉氏变换，求出单个环节所对应的传递函数，把这个传递函数写到相应的方框里面去。
在画出了这个系统的动态结构图之后， 我们继续看下面的问题：要求系统的传递函数。如何求呢？
这个系统有三个输入信号，分别是：参考输入 $r(t)$、扰动信号 $n{1}(t)$、和扰动信号 $n{2}(t)$。而我们需要求的传递函数就是分别针对于这三个输入信号的。
一般 情况下，如果没有特加说明，我们经典控制理论当中所涉及到的系统都是线性控制系统。线性系统有它非常重要的两个性质：叠加性 和 齐次性。
只有同时满足了 叠加性 和 齐次性 的系统才叫做：线性系统。
其中 这个叠加性意味着：如果这个线性系统它在多个信号的作用下，那么这个时候系统的输出就应该等于：这多个信号各自单独作用所对应输出的叠加。也就是说在这样的一个系统当中，整个系统的输出应该等于：$C(t) = C{r}(t) + C{n1}(t) + C_{n2}(t)$。
这个时候，如果我们要求某个信号单独作用所对应的传递函数，对于线性系统而言，我们可以假设：其他的输入信号都等于0.
也就是说：如果我们要求参考输入 $r(s)$所对应的输出，我们可以先假设：$n{1}(t) = n{2}(t) = 0$（表示：此刻他们都不存在，都等于零）。那么这个时候，只有参考输入信号单独作用在系统上，而求这个传递函数，我们是不是需要对这样的一个动态结构图进行简化呢？当时是可以的。但是我们更提倡大家使用Mason公式直接来做，因为Mason公式只要我们能找到前向通道，找到独立回路，这个时候多么复杂的系统，它的传递函数我们都可以很容易的获得。
比如说，我们现在来求：参考输入作用下，系统的传递函数（$\frac {C(s)}{R(s)}$），我们来观察一下：从参考输入到系统的输出，所经过的前向通道只有一个。这条前向通道它的增益是多少呢？就等于：这条前向通道所经历的所有环节传递函数的乘积。
$$n{1}(t) = n{2}(t) = 0$$ $$P{1} = K{1} \cdot \frac {1}{Ts} \cdot \frac {K{0}}{s(s+1)} = \frac {K{0}K_{1}}{Ts^{2}(s+1)}$$
好了前向通道只有一条。接着我们在来看看独立回路：在这个系统中，它存在两个独立回路。
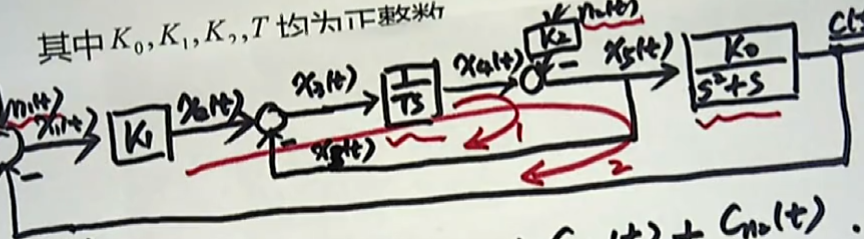
这两个回路所对应的回路增益分别是多少呢？
首先看回路1。回路1所对应的回路增益它等于：
$$L{1} = -\frac{1}{Ts}$$ $$L{2} = -K{1} \cdot \frac {1}{Ts} \cdot \frac{K{0}}{s^{2} + s} = -\frac {K{0}K{1}}{Ts^{2}(s+1)}$$
而且我们发现：这个两个回路之间有相互接触的部分，所以我们很容易的得到这个系统的特征多项式等于：
$$\triangle = 1 - L{1} - L{2} = 1 + \frac {1}{Ts} + \frac {K{0}K{1}}{Ts^{2}(s+1)}$$
这条系统只有一条前向通道，而且这条前向通道和两个回路多有接触部分，所以它所对应的余因式就等于1：
$$\triangle _{1} = 1$$
这样话，我们可以得到这个系统在参考输入信号作用下，系统的传递函数等于：前向通道增益乘上它所对应的余因式 比上 系统的特征多项式。
$$\frac {C(s)}{R(s)} = \frac {P{1}\cdot \triangle {1}}{\triangle} $$
将 $\triangle$ 、$P{1}$、$\triangle{1}$ 代入上式，也就等于：（整理）
$$\frac {C(s)}{R(s)} = \frac {P{1}\cdot \triangle {1}}{\triangle} = \frac {K{0}K{1}}{Ts^{2}(s+1) + s(s+1) + K{0}K{1}}$$
这给式子就是我们来求的第一个传递函数（$\frac {C(s)}{R(s)}$）。
我们发现，这是一个三阶系统。（其实，我们在微分方程组里面也能发现。构成这个微分方程有一个1阶的，有一个2阶的 ，这些信号（x1、x2、x5）之间是彼此串联的。所以：这个是一个一阶系统串联了一个二阶系统，构成了一个三阶系统。）
接下来我们再来看看，在扰动信号 n1 作用下的传递函数。
当我们求扰动信号作用下的传递函数，我们此时可以假设 ：参考输入信号等于零，另外一个扰动信号也等于零（$r(t) = 0 、 n_{2}(t) = 0$）。
这个时候我们来观察，从扰动信号n1输入到系统的输出C，我们发现，n1 和 r 所处的位置是完全一样的，所以n1的传递函数是和r的传递函数是完全一样的。（$\frac {C(s)}{R(s)}$ 已经求得了。）
$$\frac {C(s)}{N_{1}(s)} = \frac {C(s)}{R(s)}$$
现在再来看 n2 的传递函数。求这个扰动的传递函数，我们可以先假设，r 和 n1 的参考输入都不存在。即等于零（$r(t) = 0 、 n_{1}(t) = 0$）。
从n2 到达系统的输出，它所通过的前向通道，我们发现只有一个。
这条前向通道的增益等于：
$$P{1} = - K{2} \cdot \frac {K_{0}}{s(s+1)}$$
再来看，系统的回路没有变。所以，不管是哪个参考信号作用下，系统的传递函数，只要系统的结构不变，它的传递函数的分母多项式，也就是系统它的特征多项式是不会发生改变的。 （这一点，我们会在结果中，会得到验证。）
我们现在在观察，从 n2 到输出 c ，它的前向通道前面也有和两个回路相互接触的部分，所以对应的余因式仍然是等于1。
$$\triangle_{1} = 1$$
因此，所对应的传递函数，仍然等于：（分母是刚刚求出来的特征多项式。）
$$\frac {C(s)}{N{2}(s)} = \frac {P{1}\cdot \triangle _{1}}{\triangle}$$
$$\frac {C(s)}{N{2}(s)} = \frac {- K{2} \cdot \frac {K{0}}{s(s+1)}}{1 + \frac {1}{Ts} + \frac {K{0}K_{1}}{Ts^{2}(s+1)}}$$
这样，我们对这样的单输出多输入的系统， 对每一个输入信号作用下的传递函数，我们都很容易获取了。
总结：
这道题，我们要掌握这样几个问题：
- 首先是怎么样从微分方程来建立动态结构图，这种建立只要按照信号流动的单向性，我们把每一个方程所对应的典型的环节都画出来，然后按照信号流图的单向性，相互连接。整个系统的动态结构图，我们就知道了。
- 建立起了动态结构图以后，只要能够牢牢的把握线性系统的叠加性原理，那么每一个信号单独作用下的传递函数，我们就知道了。
再来一道例题
系统的方框图如下，试求系统的闭环传递函数。
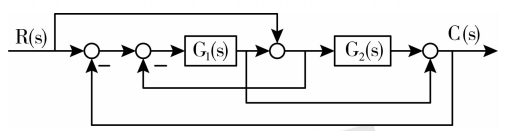
题型分析：本题是从结构图求传递函数的一般题型，这种题型一般有三种方法可以解决：即结构图变换、Mason 公式，以及变量代换的方法。
解题：
给了我们系统的动态结构图，让我们求系统的闭环传递函数。
一般，遇到这样的题型，我们的解决办法有三种：
1 . 我们可以通过对动态结构图进行化简，从而求得系统的闭环传递函数。但是这种方法在遇到了一些问题的时候， 并不好用。什么样的问题呢？ 在这个题当中，涉及到了引出点和比较点。
（引出点，比较点，引出点）
它们之间是相互交叉的，也就是说：不管我们是做比较点的前移和后移，还是做引出点的前移和后移，是必会经过一些比较点或者是引出点。那么在这个时候，就非常容易出错。所以，这种方法只有对一些简单的动态结构图，我们可以采用。如果遇到较为复杂的，像现在这种，引出点和比较点相互交叉的情况下呢，我们不提倡大家用这种方法。
2 . 还有一种方法，就是使用 Mason 公式的方法。这种方法，不管针对于动态结构图也好，信号流图也能使用。我们只要在动态结构图或者信号流图当中，能够找到从输入到输出所对应的前向通道以及所对应的单独回路，那么这个时候，牢记公式就应该可以很容易的求解系统的传递函数。
3 . 第三种方法：变量代换。它和我们高中学过的代数很像。我们之前讲过：构成系统动态结构图的环节有三种：比较点、引出点、还有方框。比较点相当于我们代数运算当中的加或者减，而方框相当于我们代数运算当中的乘法。所以，我们只要运用一些中间变量，把我们的方框也好，比较点也好，还原为原来的代数运算。那么这个时候，只要列出来了所对应的这组代数方程，消去中间变量，就可以求得系统的传递函数。但是这种方法不是我们在大学阶段应该掌握的，所以就不提倡大家使用。
所以这样的话，只要遇到了动态结构图的化简或者 信号流图的化简，我们提倡大家就使用Mason公式。
那么对于这道题，我们来观察一下，我们现在要求系统的闭环函数，这个时候，系统的输入信号是r(s) ，输出信号是 c(s) 。从输入到输出，所进过的前向通道有几条？有三条 。
第一条前向通道：
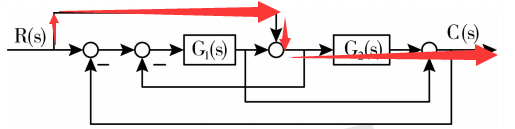
所对应的前向通道的增益是：$P{1} = G{2}(s)$ 。
前向通道的增益的求法：我们使用前向通道所进过的所有环节所对应的传递函数乘起来，就是该前向通道的通道增益了。
第二条前向通道：
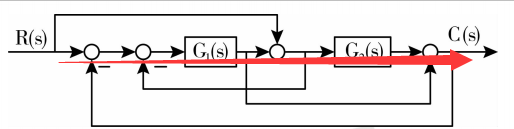
所对应的前向通道的增益是：
$$P{2} = G{1}G_{2}$$
第三条前向通道：
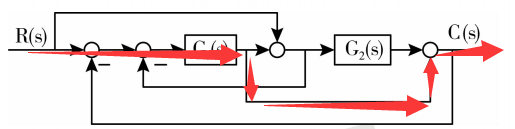
所对应的前向通道的增益是：
$$P{3} = G{1}$$
现在，前向通道现在我们找完了。现在看看系统当中有没有回路。首先，我们来观察一下，这有一个小回路
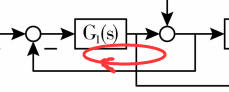
所对应的回路增益，我们使用 $L_{1}$ 来表示：
$$L{1} = -G{1}$$
除了这个小回路之外，还存在一个大回路，$L_{2}$
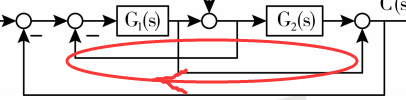
它所对应的回路增益是：
$$L{2} = -G{1}G_{2}$$
第三个回路：
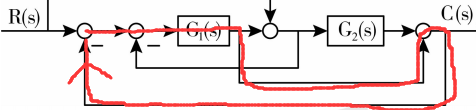
增益：
$$L{3} = -G{1}$$
按照回路的定义，信号的流动都是单项流动的，所以所有的回路我们就找完了。
（注意： 往往我们习惯犯的错误是：先把动态结构图转换为信号流图，再在信号流图中使用Mason公式。这个时候就非常容易出现一种错误。我们拿到了动态结构图之后，我们不提倡把它转为信号流图，我们只需要在动态结构图中，使用信号流图的单向性来找前向通道，来找独立回路，就可以了）
刚刚，我们已经找到了前向通道和独立回路， 那么这个时候，我们观察这三个独立回路之前在下面这段是相互接触的。所以不存在两两或者三三互不接触的回路。
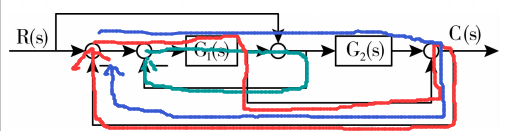
因此，所对应的特征式就等于：
$$\triangle = 1 = L{1} - L{2} - L{3} = 1 + 2G{1} + G{1}G{2}$$
而我们刚才的三条前向通道，它和我们三个回路之间都存在相互交叉的部分，因此所对应的余因式 都等于 1。
$$\triangle{1} = \triangle{2} = \triangle_{3} = 1$$
这样，整个系统的闭环传递函数，我们就很容易的可以获得。（利用了 Mason 公式 ）
$$\varphi(s) = \frac {C(s)}{R(s)} = \frac {P{1} \triangle{1} + P{2} \triangle{2} + P{3} \triangle{3}}{\triangle} = \frac {G{2} + G{1}G{2} + G{1}}{1 + 2G{1} + G{1}G_{2}}$$
总结：
这个系统一定要是一个线性系统。只要是线性系统，它就一定满足叠加性的原理。
所谓的叠加性：在参考给定，以及扰动输入共同作用下的输出，就应该等于，参考输入单独作用下的输出 叠加上 扰动输入单独作用下的输出。
而在分布求他们各自的传递函数的时候，我们要把握一点，求某一个信号单独作用的时候，我们要假设其他的输入是等于0的。